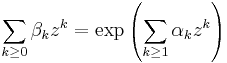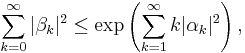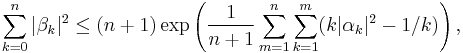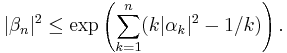Lebedev–Milin inequality
In mathematics, the Lebedev–Milin inequality is any of several inequalities for the coefficients of the exponential of a power series, found by Lebedev and Milin (1965) and Isaak Moiseevich Milin (1977). It was used in the proof of the Bieberbach conjecture, as it shows that the Milin conjecture implies the Robertson conjecture.
They state that if
for complex numbers βk and αk, and n is a positive integer, then
See also exponential formula (on exponentiation of power series).
References
- Conway, John B. (1995), Functions of One Complex Variable II, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94460-9, OCLC 32014394
- Korevaar, Jacob (1986), "Ludwig Bieberbach's conjecture and its proof by Louis de Branges", The American Mathematical Monthly 93 (7): 505–514, doi:10.2307/2323021, ISSN 0002-9890, JSTOR 2323021, MR856290
- Lebedev, N. A.; Milin, I. M. (1965), "An inequality", Vestnik Leningrad University. Mathematics 20 (19): 157–158, ISSN 0146-924x, MR0186793
- Milin, I. M. (1977), Univalent functions and orthonormal systems, Providence, R.I.: American Mathematical Society, MR0369684 (Translation of the 1971 Russian edition)